Lec-7 backpropagation - Machine learning (台大李宏毅)
本文为台大李宏毅的机器学习入门课程笔记。
第七章:反向传播
重点:
- 链式法则
- forward pass
- backward pass
Back-propagation 其实就是针对NN的gradient descent,只是如果直接把gradient descent 用在NN上就会没有效率,因为可能有几百万个参数要优化,那就会卡死。所以就用链式法则来进行优化,也就是这个backpropagation。
Chain rule 链式法则

如果对w计算偏导,就可以只计算对某一个参数的loss 来计算
其中,$C^n$ 看作一个衡量$y^n$与$\hat y^n$之间距离的函数,越小越好
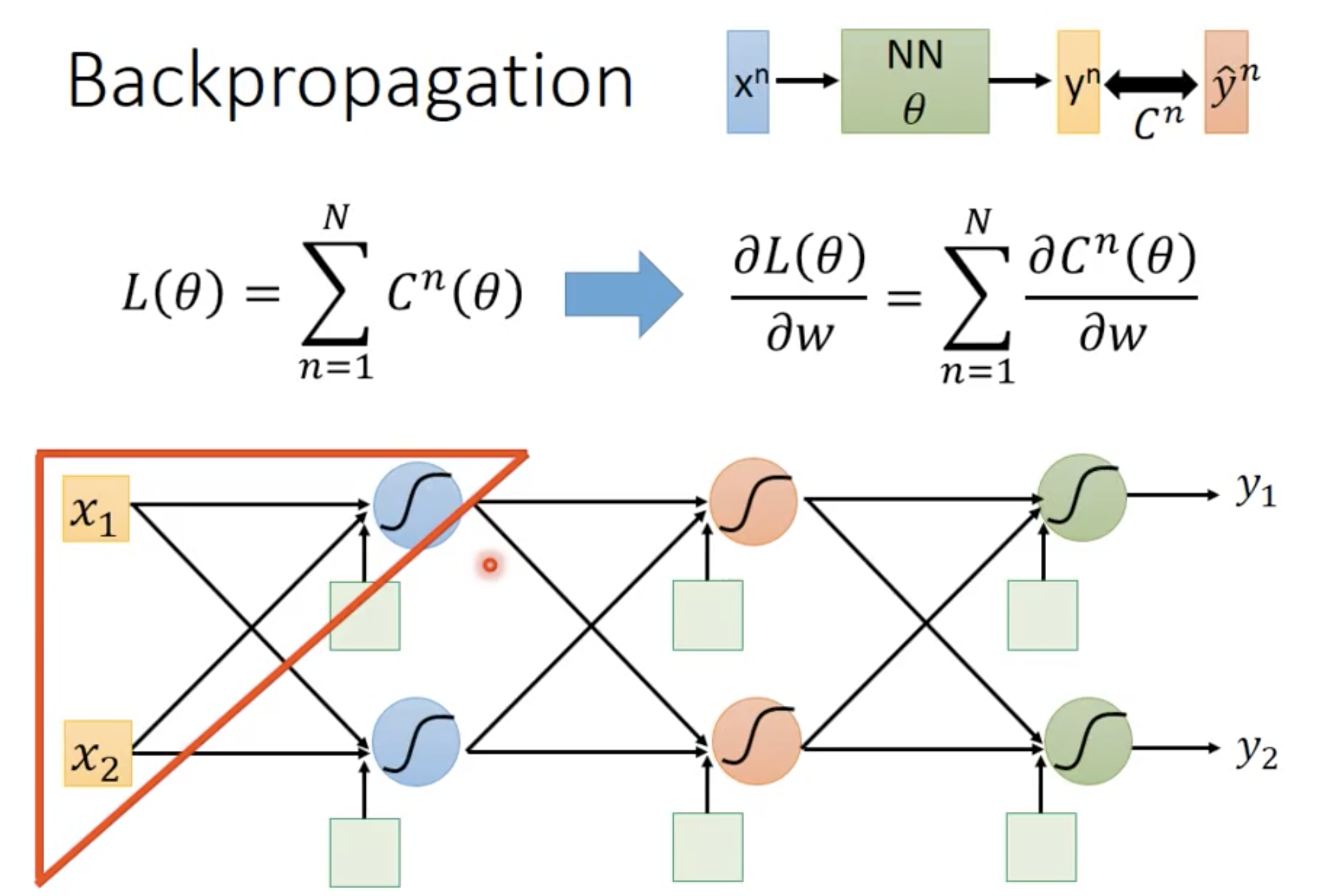
接下来我们只看红框里面的内容
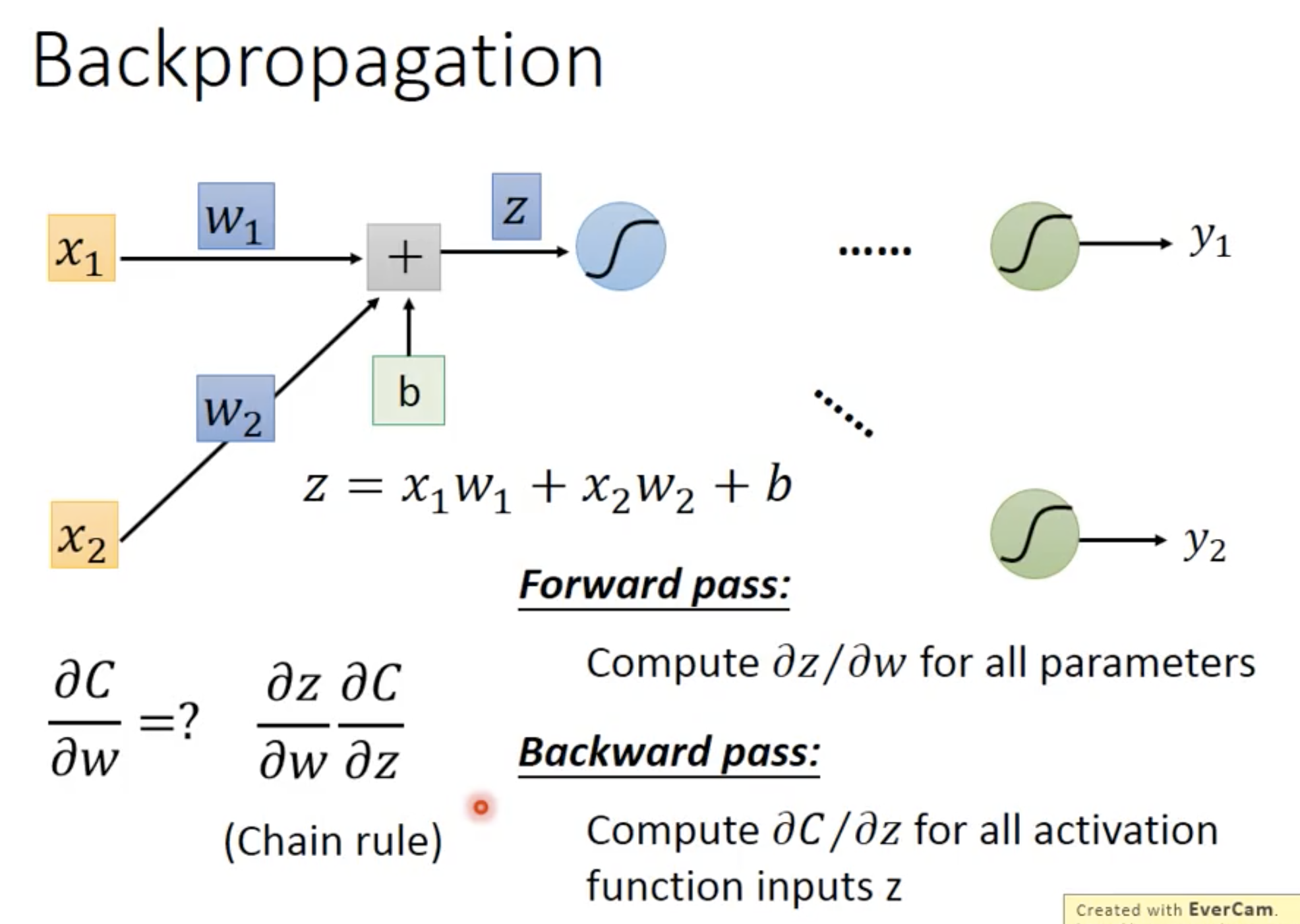
可以看到,$\frac {\partial C}{\partial w}$ 可以被链式法则拆解成 $\frac {\partial z}{\partial w}$ 和$\frac {\partial C}{\partial z}$
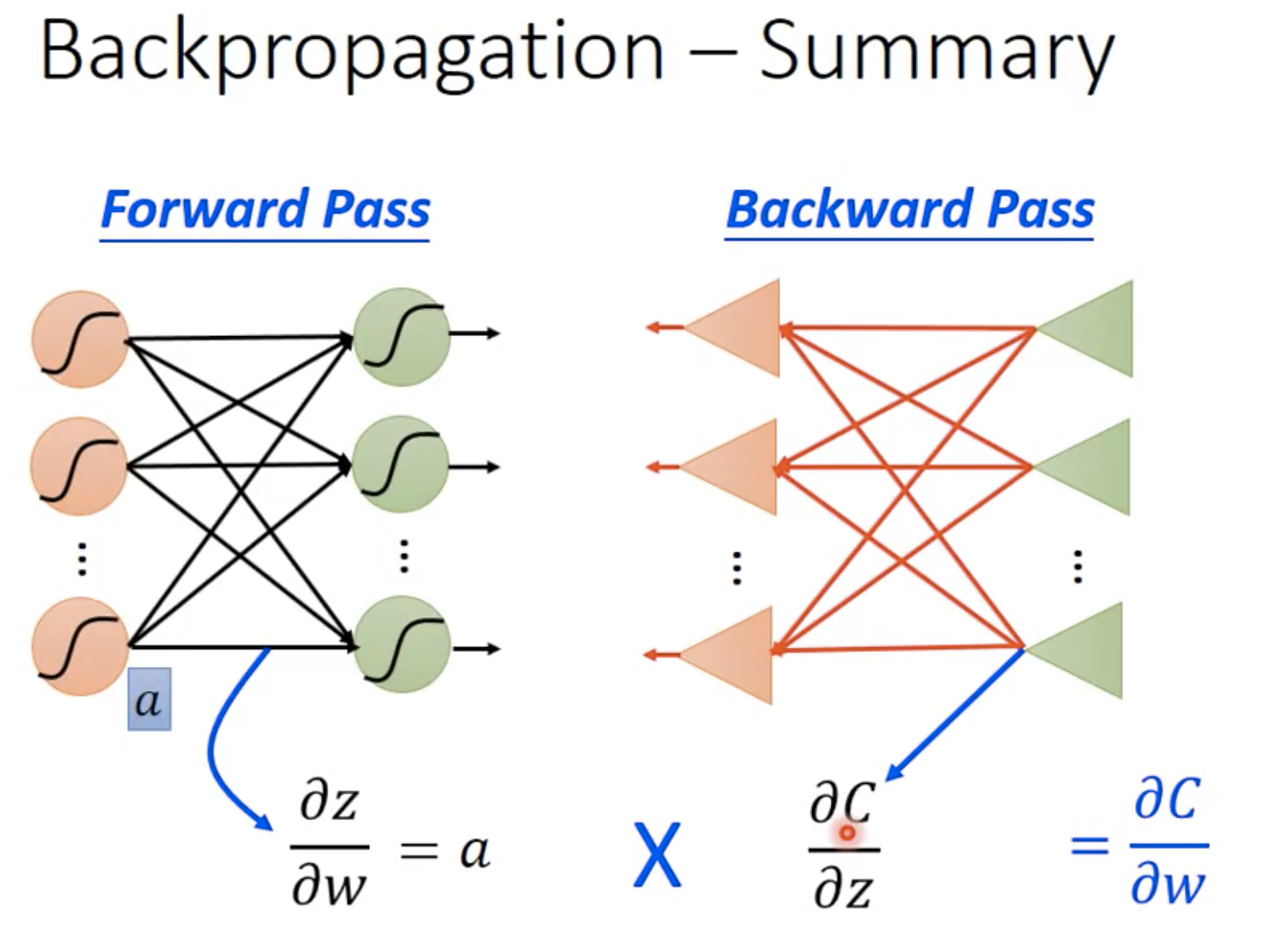
其中,前者被称为forward pass, 后者被称为backward pass。
Forward pass 前向传播
可以很容易地发现,w1对z的偏导就是x1, w2对z的偏导就是x2。也就是说,偏导只取决于输入。举个例子:
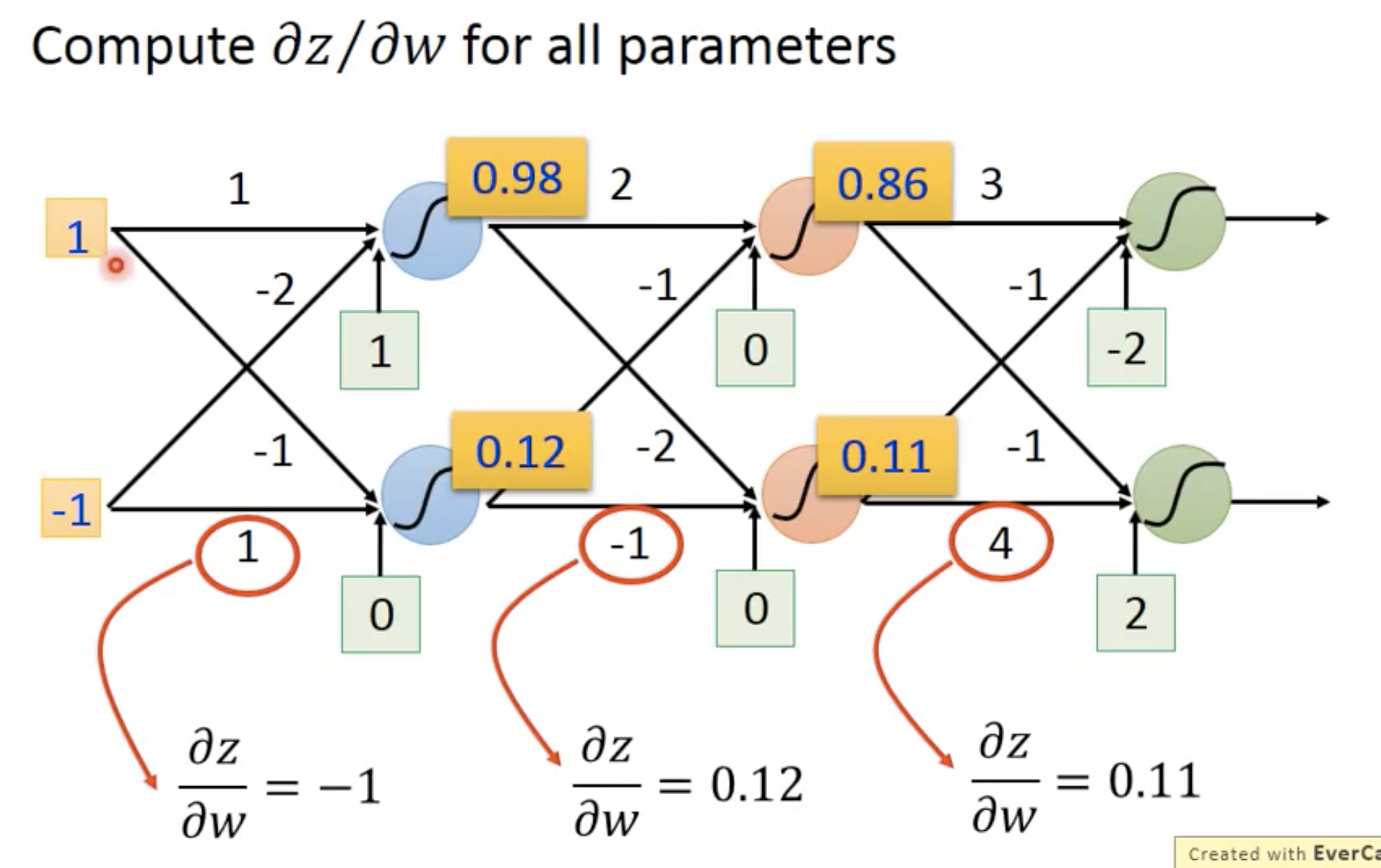
这个步骤就叫做forward pass,它很容易就能得出来
Backward pass 后向传播
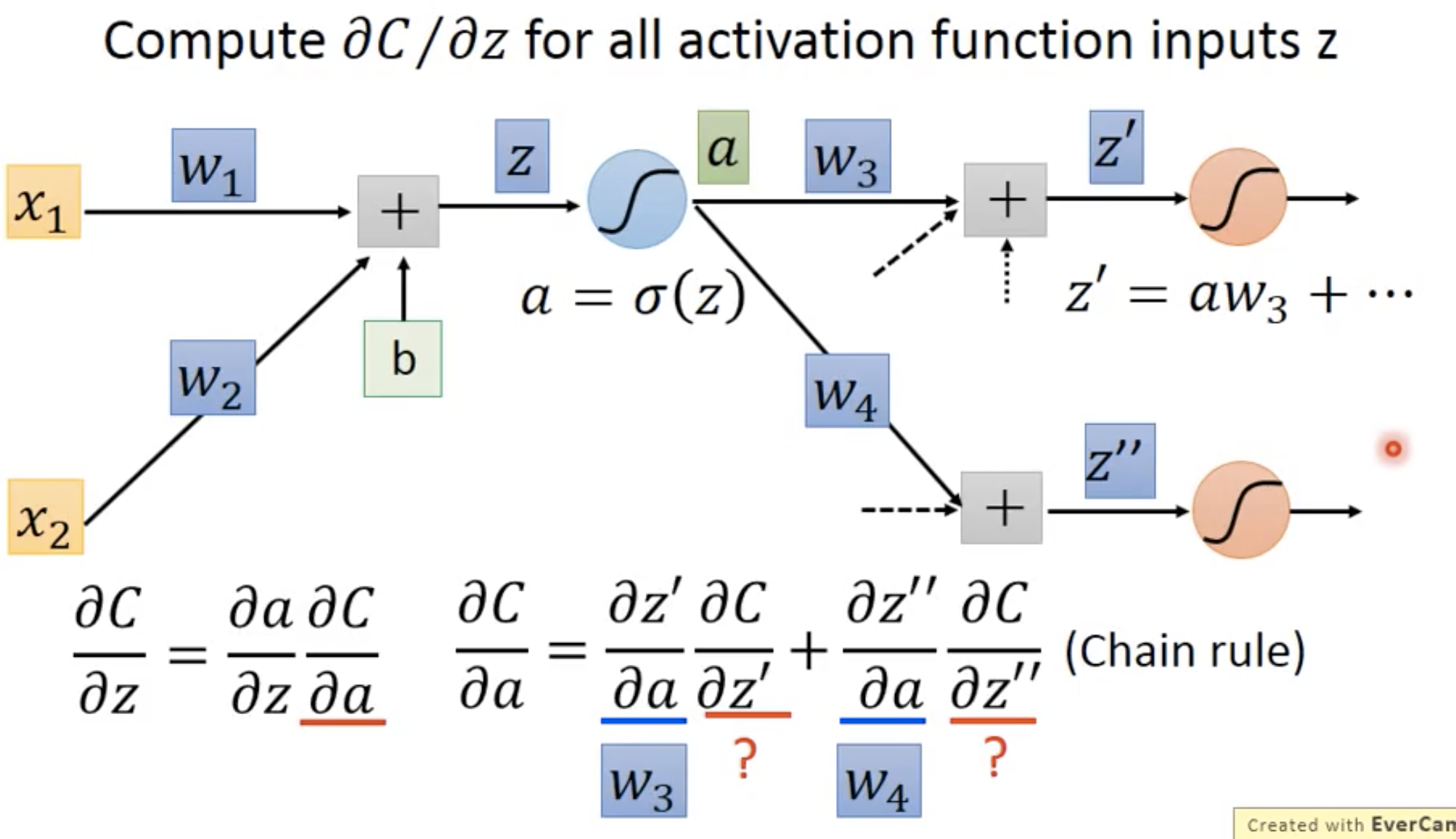
尽管我们知道a对z’ 的偏导和a对z‘’的偏导都能算出来(就是它们对应的权重),但我们不知道z’对C和z’’对C的偏导(因为我们不知道z’、z’’对C的关系,因为之后还有经过很多操作)。
但是我们假设我们知道了,就直接把它们带入运算。
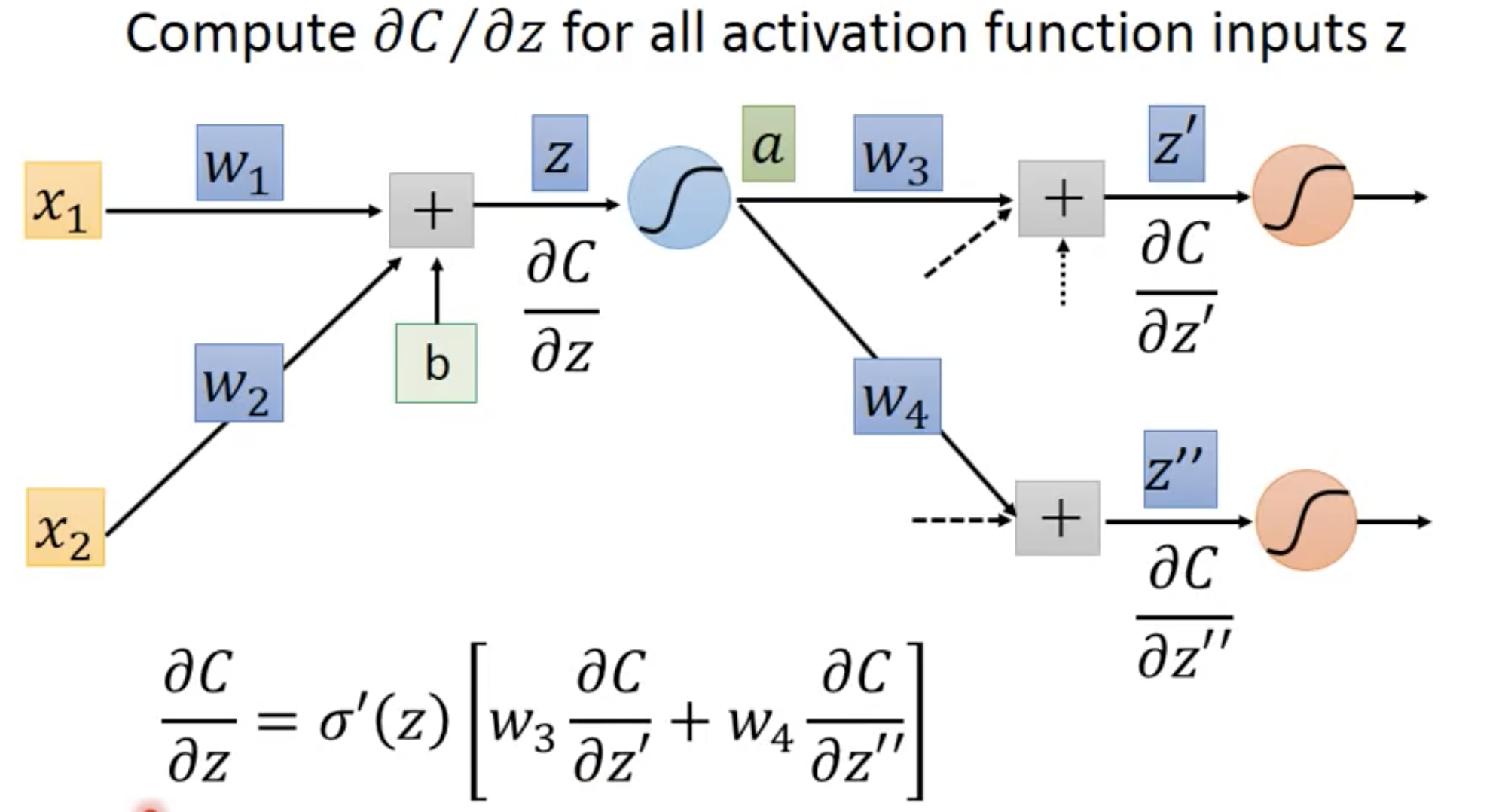
让我们反着来看这件事:
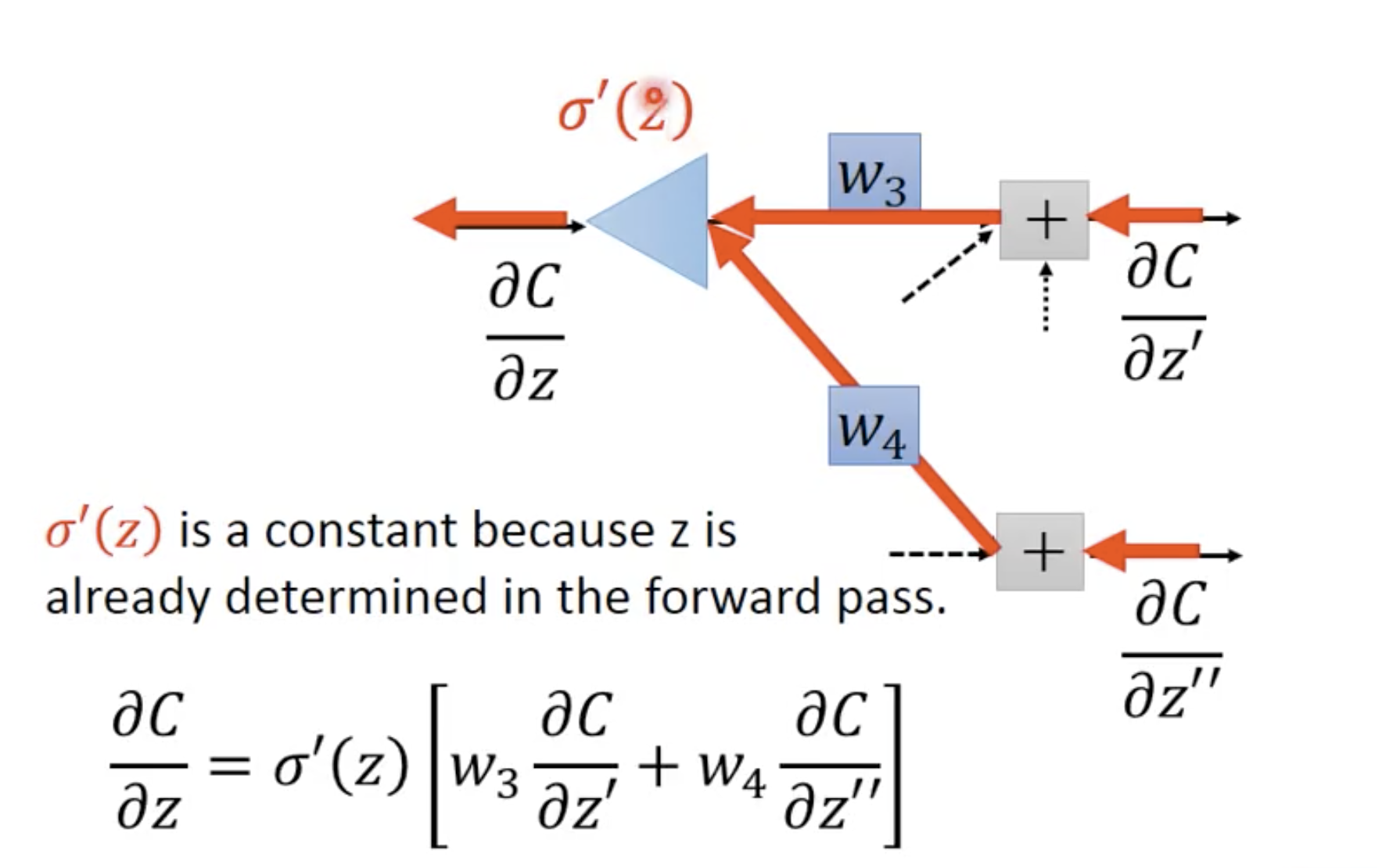
其中,z在forward pass中就已经决定好了,所以它是一个常数。
那么现在就是要算出刚刚假设是已知的那两个数就可以了,那么怎么算呢?
有两种情况:
- 这一层的输出就是输出层
- 这一层的输出不是输出层
case 1 是output
那么就可以直接得出来
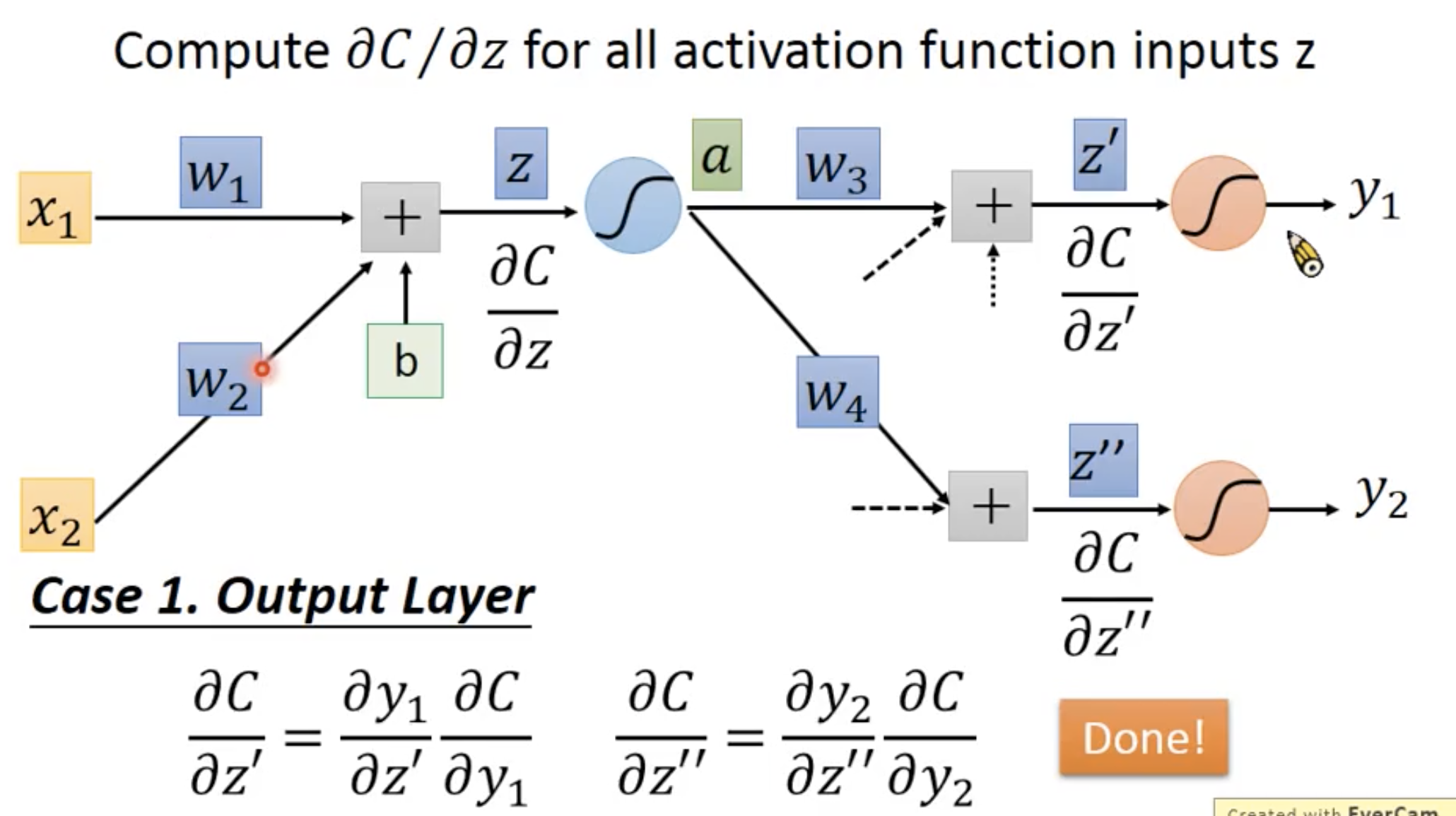
case 2 不是output layer
这种情况就需要recursive地计算,一直到reach output layer为止
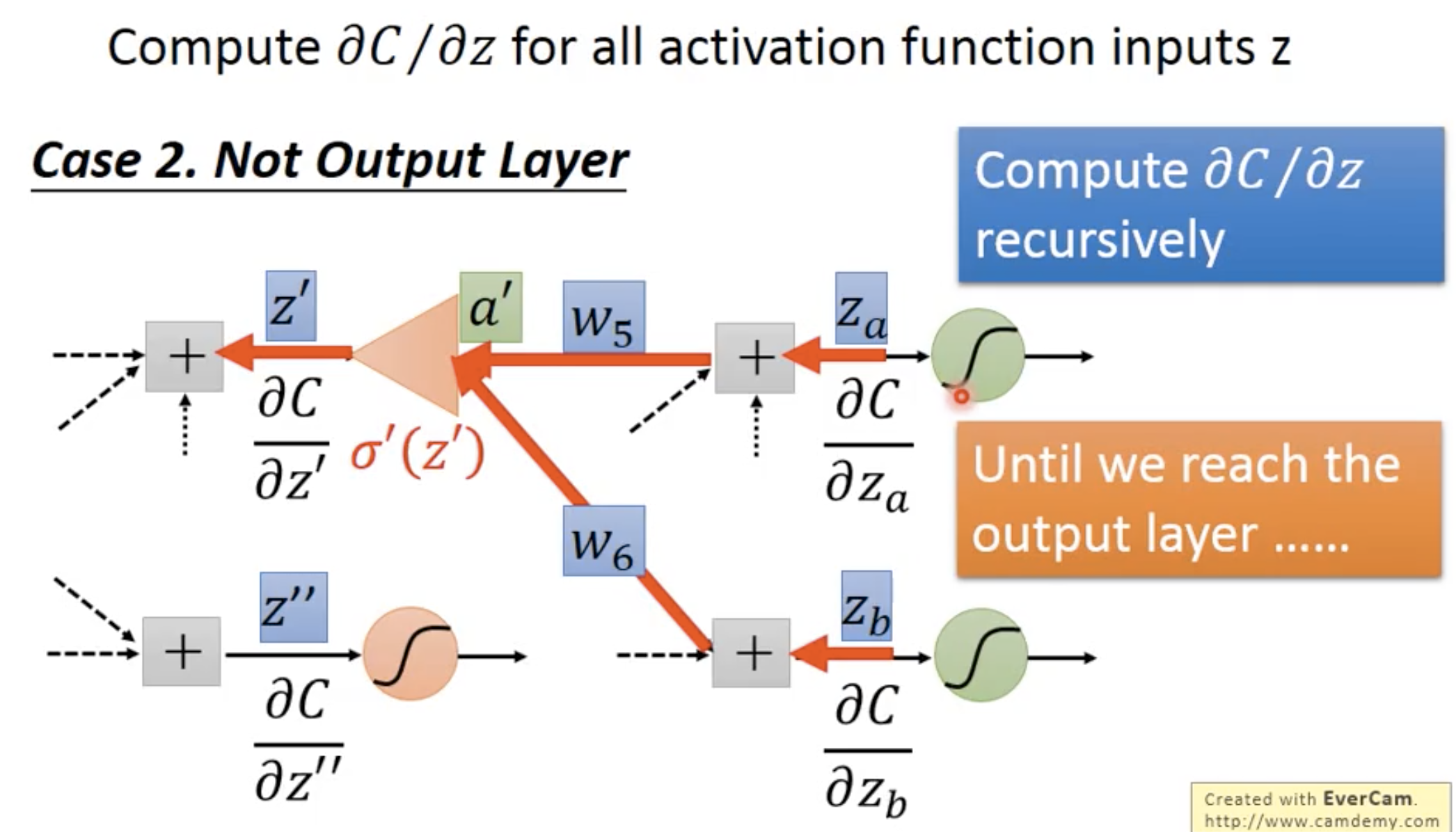
但是这样的话就没有效率。我们可以直接反向运算,即直接先从output layer进行计算,这样就不需要recursion了。也就相当于建立了一个反向的NN,这个反向的NN的输入是原先的输出,输出是原先的输入。

总结backpropagation的过程
总结来说,其实整个折腾这么两趟,是因为想知道每一个weight对最后的loss函数的偏微分。而这个偏微分根据链式法则来计算的话,中间的每一项偏微分都需要推导来计算。