Lec-5 Regression(case study) - Machine learning (台大李宏毅)
本文为台大李宏毅的机器学习入门课程笔记。
第五章:逻辑回归
重点:
- 什么是逻辑回归
- 逻辑回归 vs 线性回归
- feature transformation
- 深度学习的引入
在学了linear regression之后呢,我们就可以把logistic regression,是在linear regression 的model上又套了一个$\sigma$ ,变成一个新的model
Step 1 function
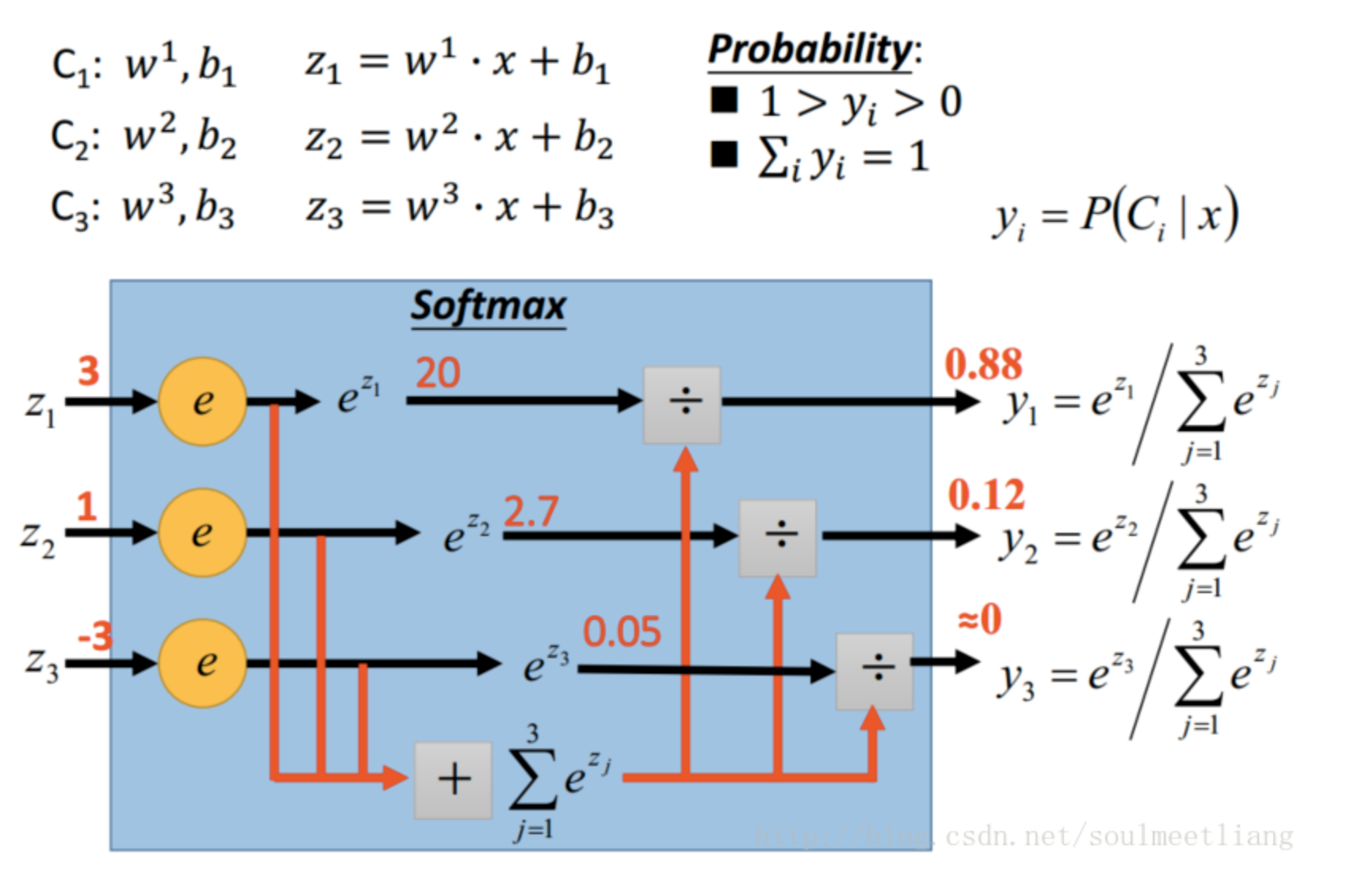
把输出的scalar当作一个几率,这个几率大于0.5 就是class 1,否则就是class 2。 当给定一个样本x,用f来计算它属于类别c1的概率,就可以预测它属于那个类别
注意,图中的$z = \sum_i{w_ix_i}$ 应改为$z = \sum_i{w_ix_i}+b$
Step 2 Goodness
与之前的loss function不同,这里的L是Likelihood的缩写,也就是似然程度。

可以看到这里的最优解是在arg max的地方。我们可以通过一个简单的变换,把它变成arg min。方法如下:(图中右上角方框中改为$\hat y ^2 = 1, \hat y ^2 = 0$)

经过这样的最大-> 最小的变换,L 就变成:
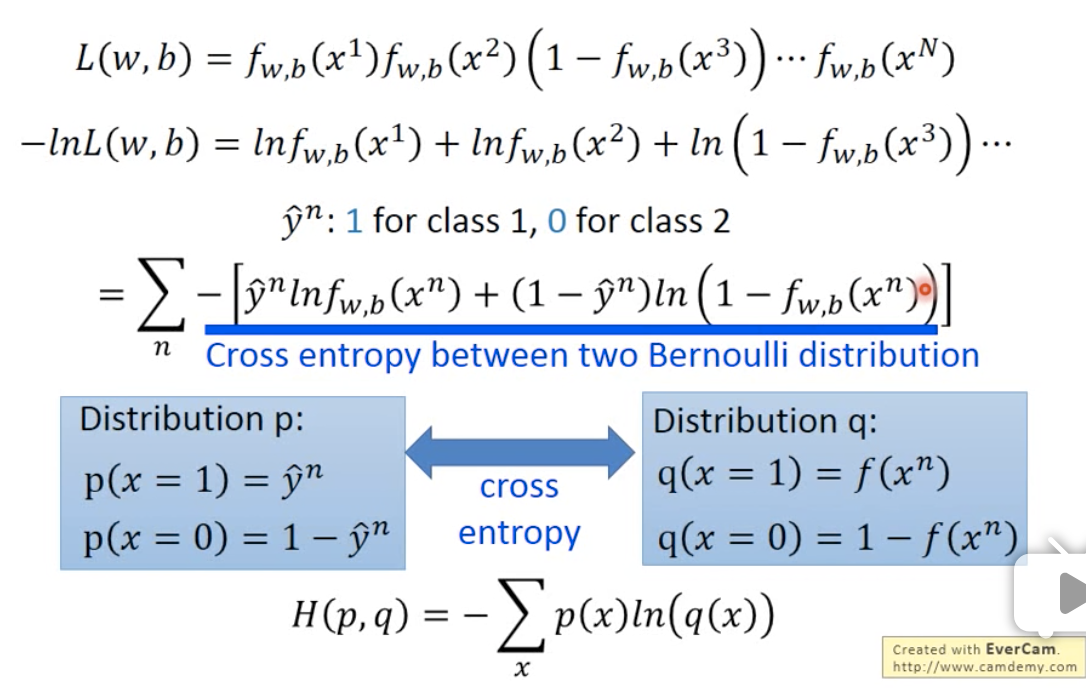
对一个training data,我们要minimize的对象,是所有的样本的cross entropy的总和。
我们把$f(x^n)$ 和$\hat y ^n$都假设为i.i.d 的伯努利分布(因为是2值),我们的目标就是希望它们的分布能越相近越好。
其中,cross entropy是一个式子,是我们想要minimize的内容。如下:
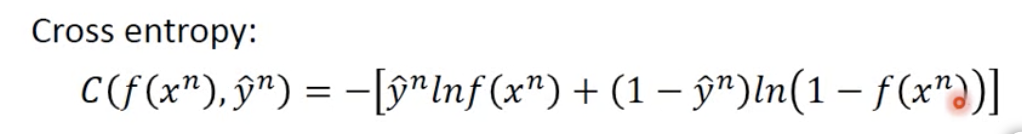
为什么不直接用mse,而要用cross entropy呢?我们后面再讲。
Step 3 Find the best function
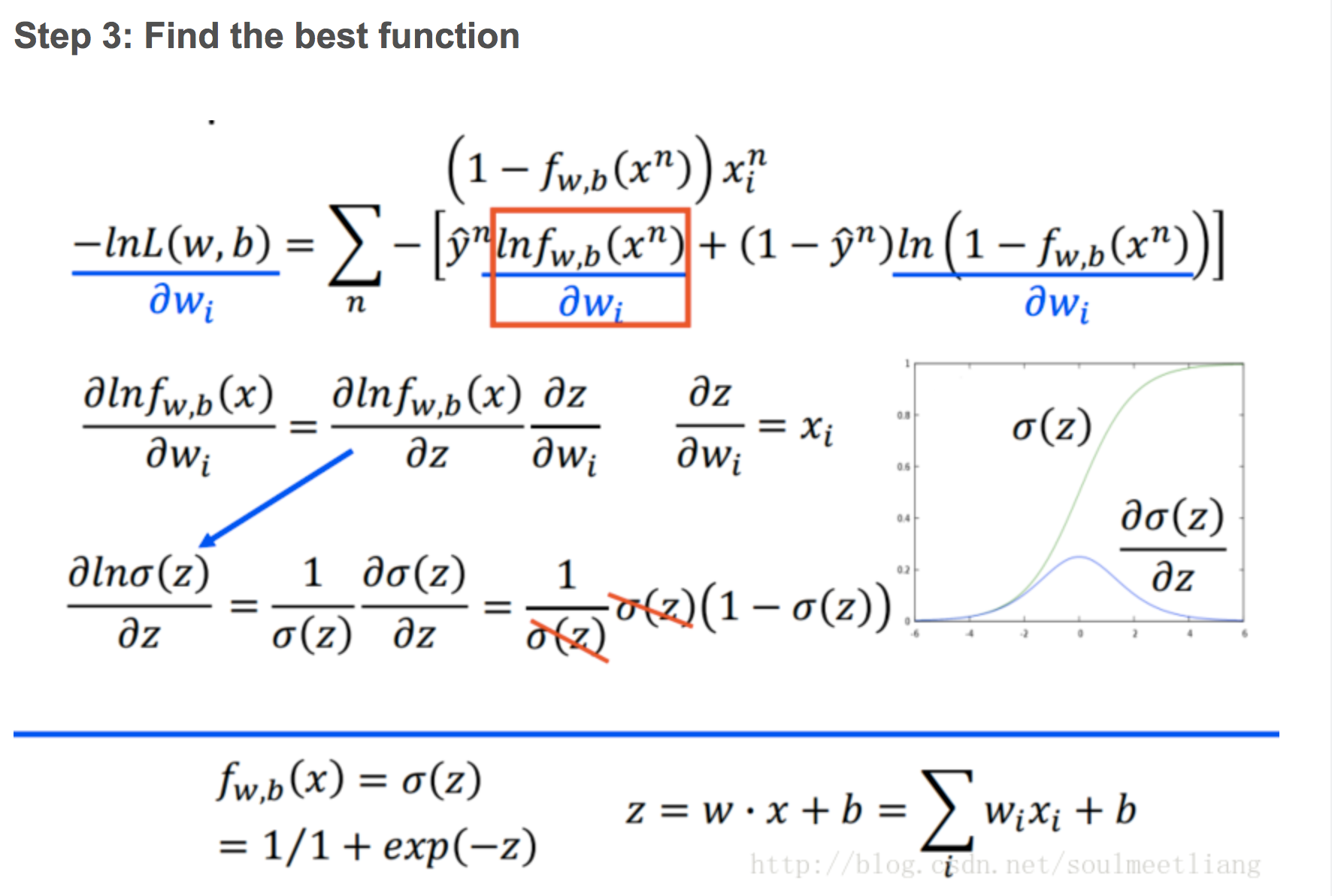
经过一通运算,我们就会发现,这个loss的函数经过转换,其实还是可以跟linear regression 相同的。(数学运算过程略过了)
Linear regression vs logistic regression
下面我们来看一下linear 和logistic regression的对比

我们可以看到:
第一步
第一步中,logistic regression是在linear的基础上,增加了一个$\sigma$使得输出的范围规范到了(0,1)之间
第二步
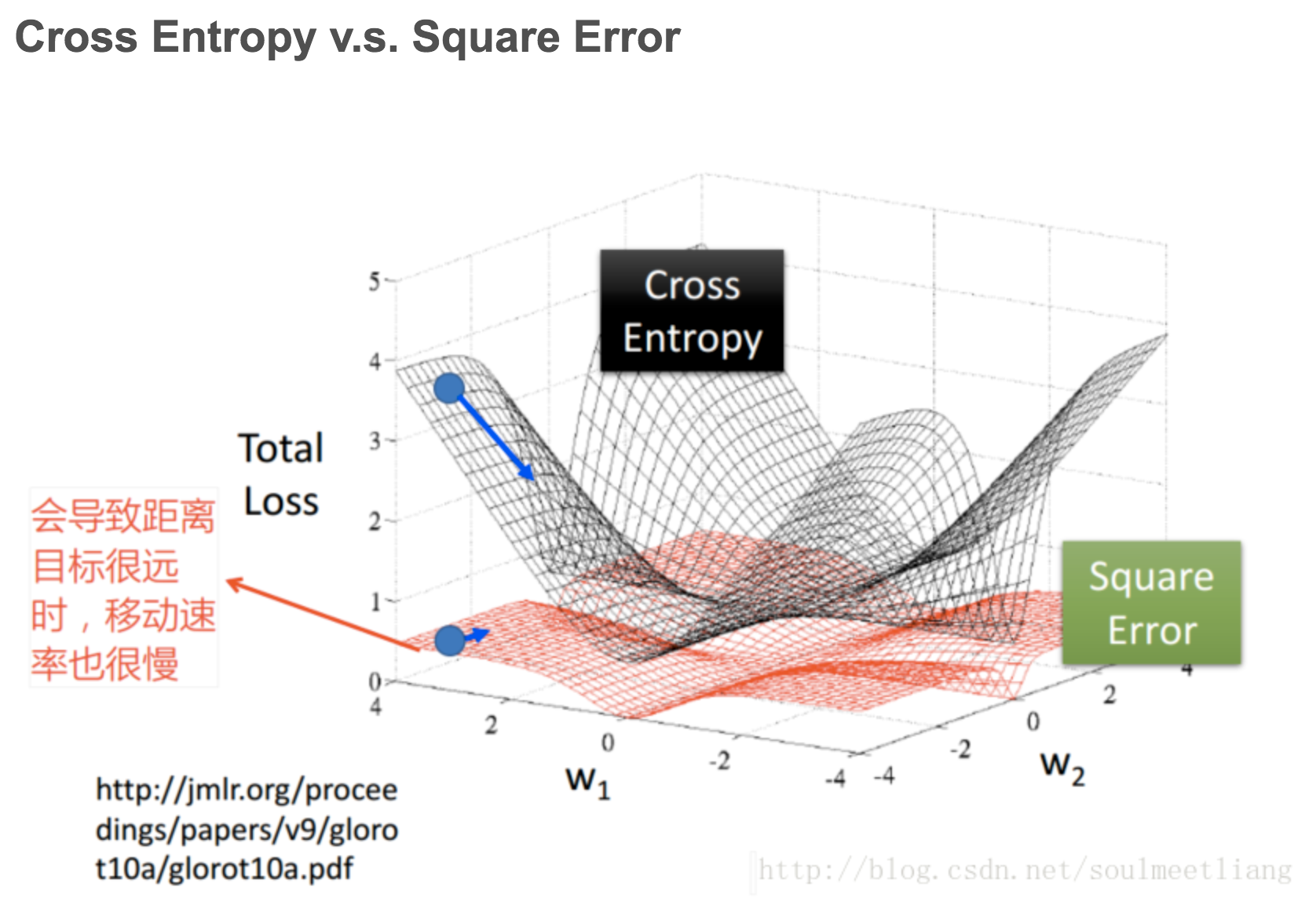
第二步中,logistic regression为什么不能用mse呢?

如果 y = 0, f = 1, 此时距离目标很远,但是微分算出来 = 0,不会再更新了!
我们将对两个参数w1,w2对两种loss画出图,如下:
假设
第三步
第三步可以看到,logistic 和linear regression一模一样。除了logistic的值是只限制在(0,1)之间。
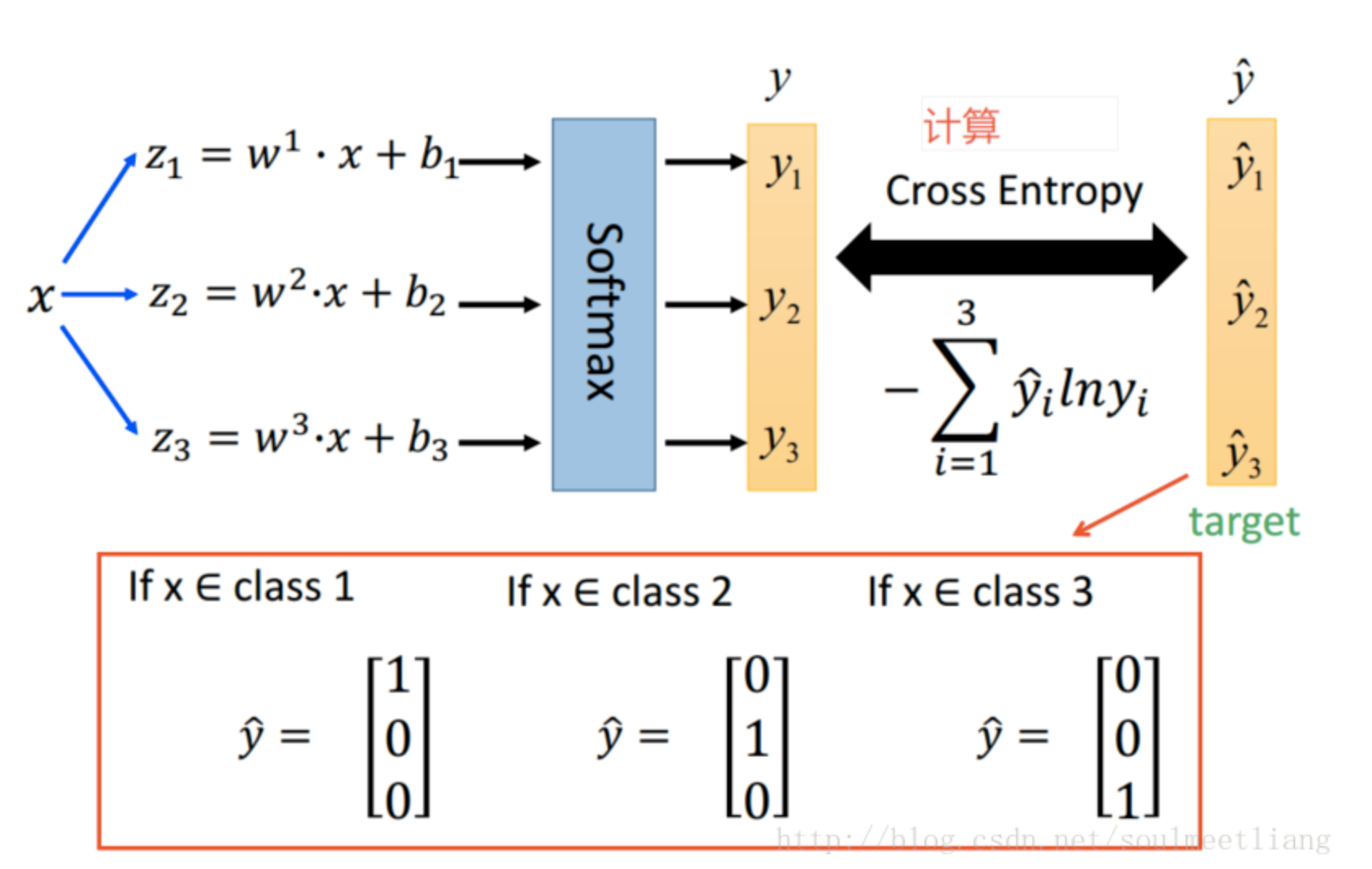
多分类