Lec-2 Regression(case study) - Machine learning (台大李宏毅)
本文为台大李宏毅的机器学习入门课程笔记。
第二章:回归-案例分析
重点:
- 什么是回归
- 如何优化回归模型
- 什么是过拟合
这节课用一个例子来讲Regression learning。
首先来熟悉一下这个例子:宝可梦升级之后的CP值预测:

Step1. Model
由于考虑这个场景,进化前和进化后的cp值分别作为输入输出,所以知道这是监督学习。我们假设一个linear model,假设为$y = b + w X_{cp}$
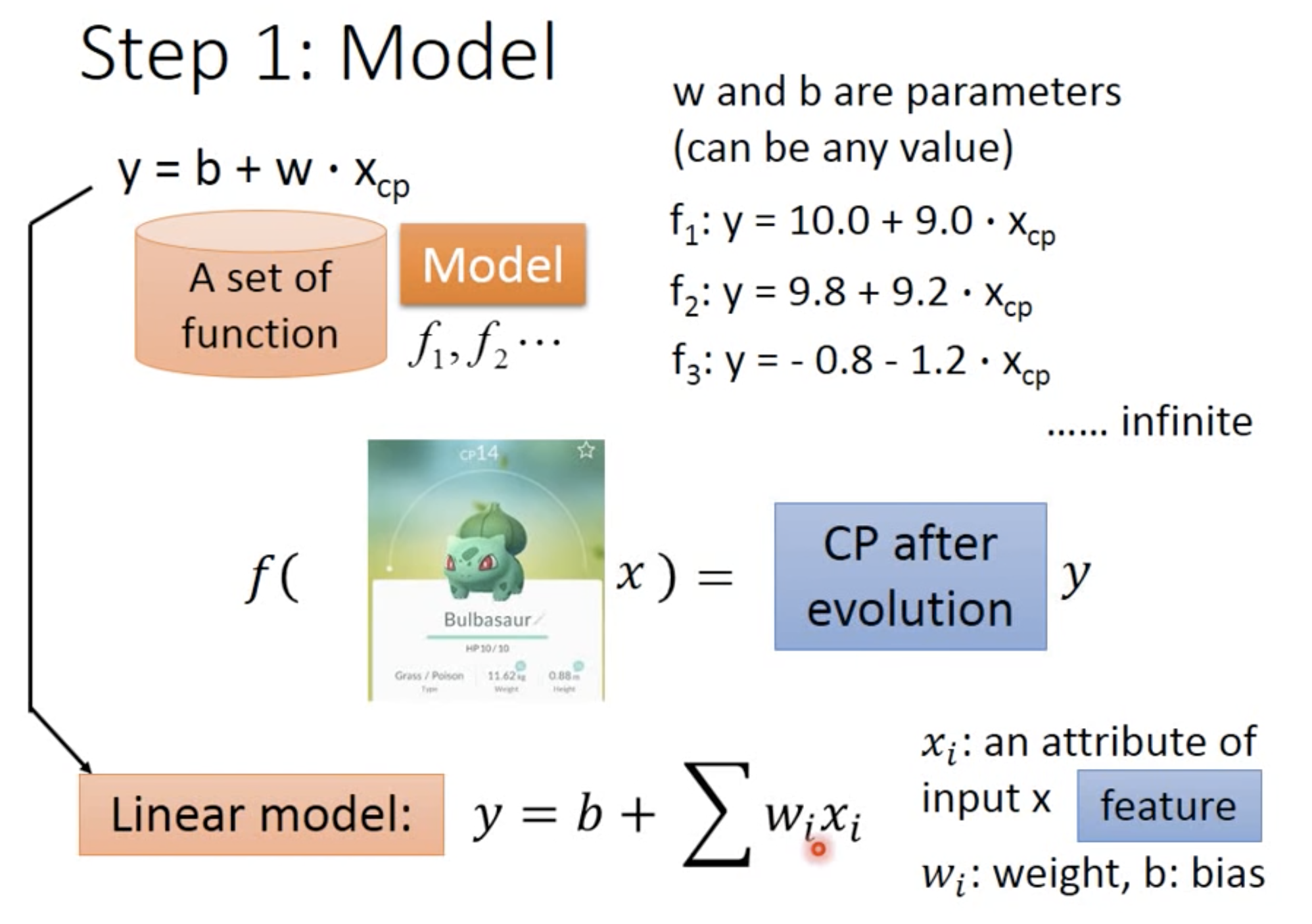
可以看到,一只宝可梦用$x$表示,它有几个刻画的维度(如身高、重量、cp值等),这些都称为feature 特征。$w_i$称为weight权重,$b$称为bias偏移量
首先,从左上角的model 盒子中选出一种linear model$y = b + w X_{cp}$,然后我们可以任意给w和b赋值(如$f_1,f_2,…$)。不同的b、w,得到的 f 不尽相同,而下面,我们就要找到最能契合要求的一个 f
Step 2. Goodness of Function
首先我们先用 输入-输出 来画个图:(红色的点是激光笔,不是数据点,忽略就行)
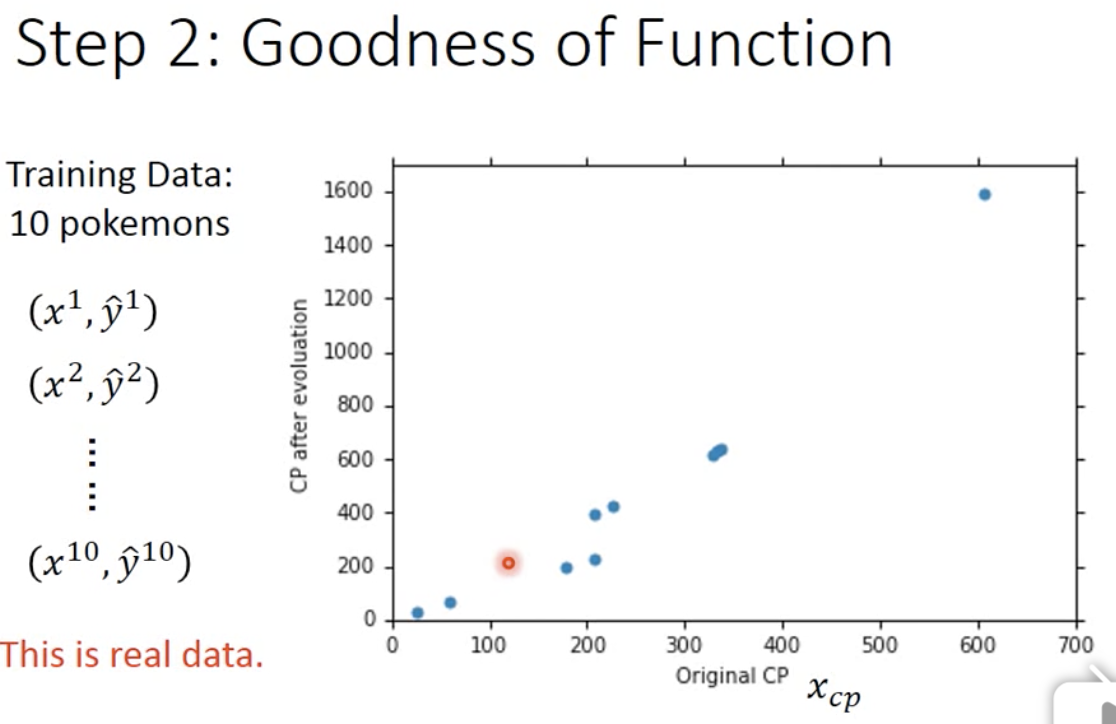
我们可以看到,输入输出之间,仿佛隐约存在一个线性关系,而这就是我们想要的。
为了选出最契合的 f ,我们要建立一个Loss function $L$ ,也就是函数的函数。我们希望这个函数$L$能够接受一个函数$f$,并告诉我们这个函数$f$有多坏
如果我们将 f 的 w 和 b 作为横轴和纵轴,则在下图中每一点都代表一个 function f ,而颜色代表$L$的output大小(红大蓝小),也就代表该 f 的好坏(越小越好)。我们可以看到,最小的点smallest对应的函数 f 就是我们想要的
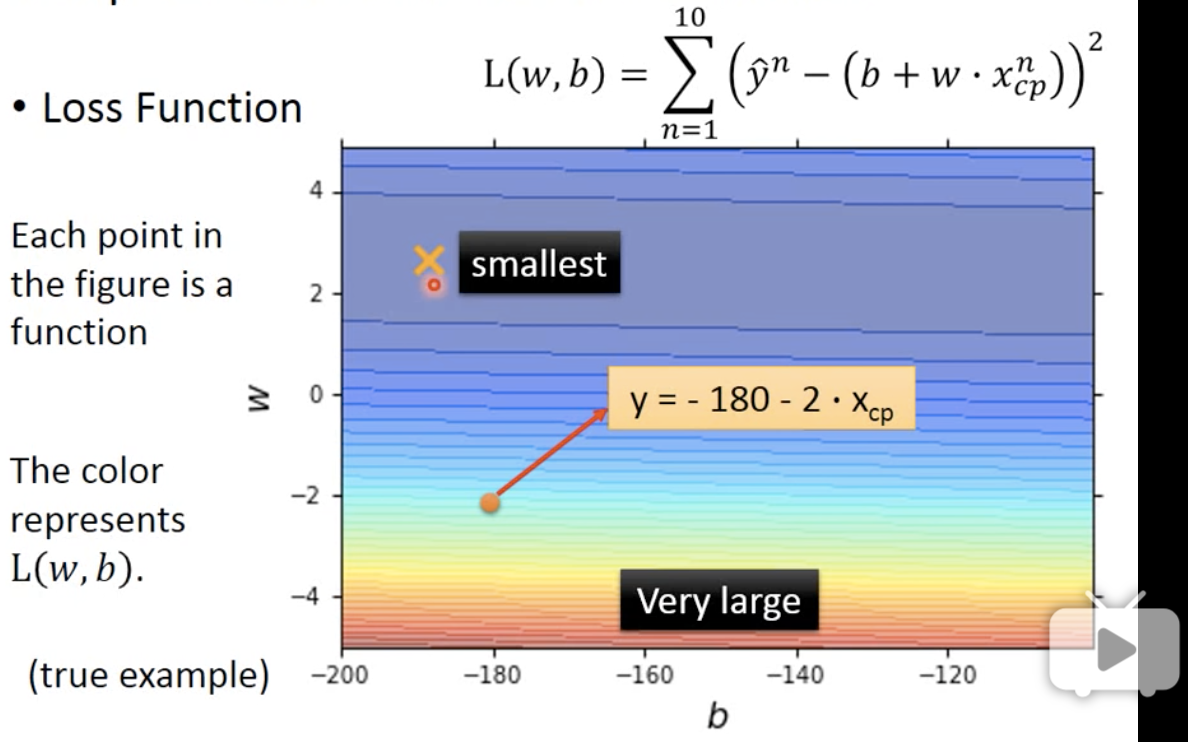
可以看到,损失函数L被定义为:
$$
L(w,b) = \sum_{n=1}^{10}{(\hat y^n - (b + w x^n_{cp}))^2}
$$
也就是用该函数$y = b + wx$预测测试集中的数据时,每个预测结果与真实结果的差值的平方的总和。对于不同的w和b,使得L最小,即为所求。
Step 3. Best Function
有了上面的损失函数,我们就知道如何来衡量一个模型的好坏。但是如何找到这个模型呢?也就是如何一步步优化得到这个结果呢?
当然,对于一个二元一次方程,我们当然可以用解方程的思想直接暴力求解。但是如果特征值很多、或者n元m次方程的时候,解方程就不能解决问题了。我们就要用到Gradient descent 梯度下降。
考虑一个只有一个参数的方程(一元一次方程)的梯度下降方法:
首先,随机选取一个初始的点 $w_0$
其次,计算微分 (切线斜率k、法向量)
- k < 0,则w应该增大
- k > 0,则w应该减小
- k = 0,停止更新
再次,决定步长。 当我们知道该往哪里踏一步之后,还要知道这一步踏多大。这个步长就叫做 learning rate $\eta$
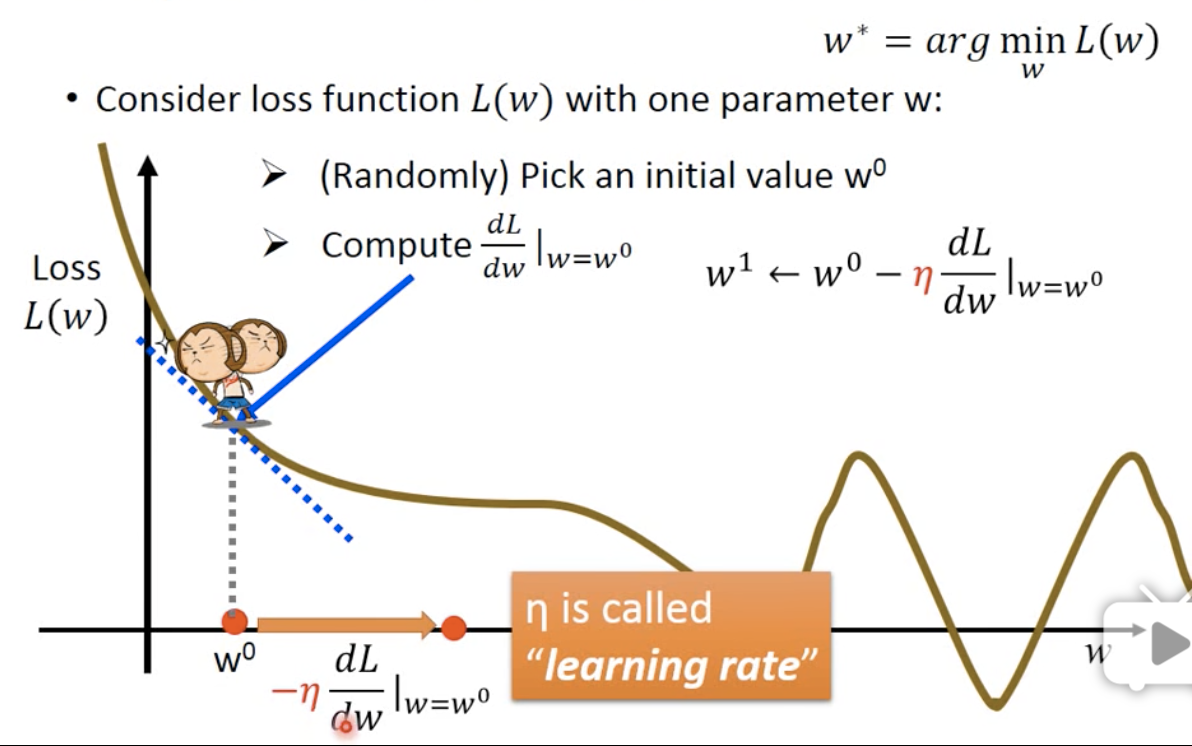
图中的横坐标是w,也就是一元方程中的元的大小;纵坐标是loss function的值。每个点就表示当w 取$x_w$时,loss function会给$f(w)$打多少分,也就是$f(w)$有多坏。
因为我们的目标是能够找到让loss function最小的w是多少,所以我们希望每次更新w的时候,都能让它的loss减少一点点。
假设我们站在图中小猴子的地方,所在的地方的斜率 < 0。 这时候我们向左看,发现如果往左沿着黄色的线走,loss就会增加,这就事与愿违了;向右看,发现黄色的线下降了,所以我们就向右走,也就是w增加。
为什么有负号 $-$ 呢?因为我们可以总结出来,当微分>0时,为了让loss减小,就需要剪去一个大于零的数;而当微分<0时,为了让loss减小,我们可以直接加上一个小于零的数。
另一个问题,每次要增加或减少多少w值呢? 有两个因素影响。第一,即微分值。如果微分值很大或很小,表示此处非常陡峭,那么证明距离最低点还有很远的距离,所以移动的距离就应该很大。第二个因素是我们事先自主定义的常数项 $\eta$ 值,即步长, 也是learning rate。
按照这个模式,不断重复,经过非常多的参数更新后,能达到一个最低点。
值得注意的是,这个最低点,有可能不是全局最优解,而只是局部最优解。但是幸运的是,在linear regression 这种模型上,不会出现这种问题。因为linear model 的loss 不会有global optimal。
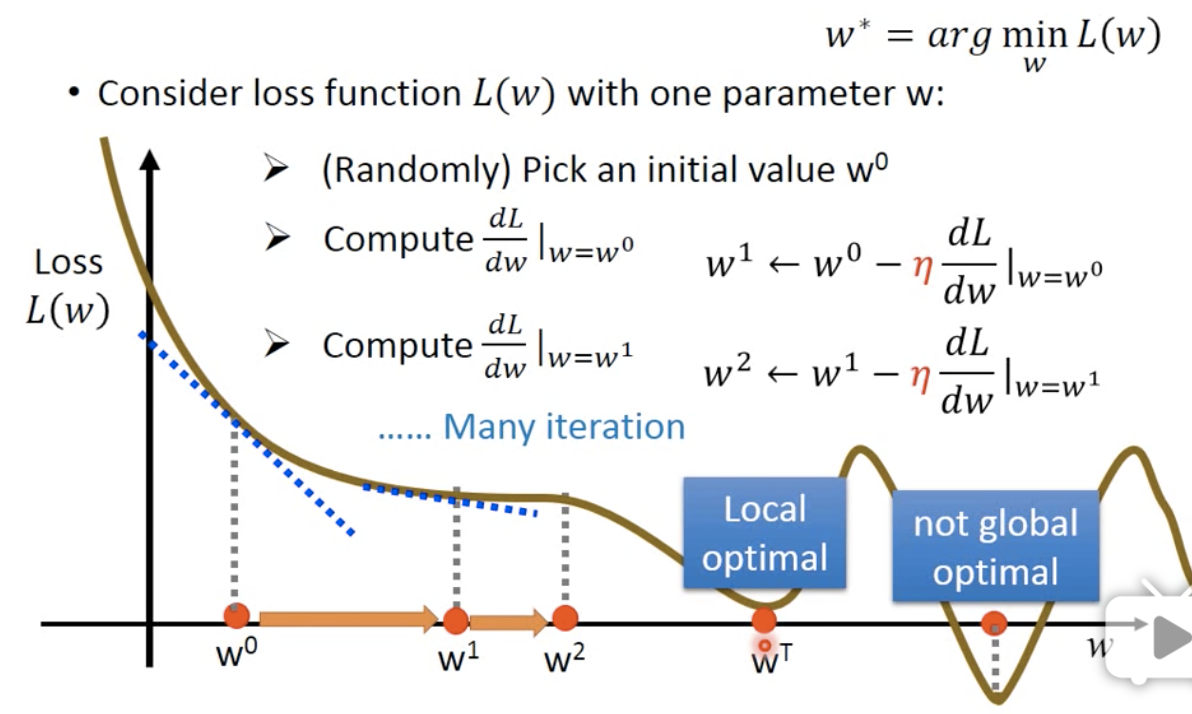
这是一个参数的情况,那么如果有两个参数呢?
当我们有多个feature时,即不仅有 w 还有 b ,同样不会影响梯度下降过程。

需要补充一下,gradient descent 中的gradient是什么呢?就是右上角红色框框里的偏微分
Result
通过前面的三个步骤,我们找到了一个最佳的f。那么结果怎么样呢?
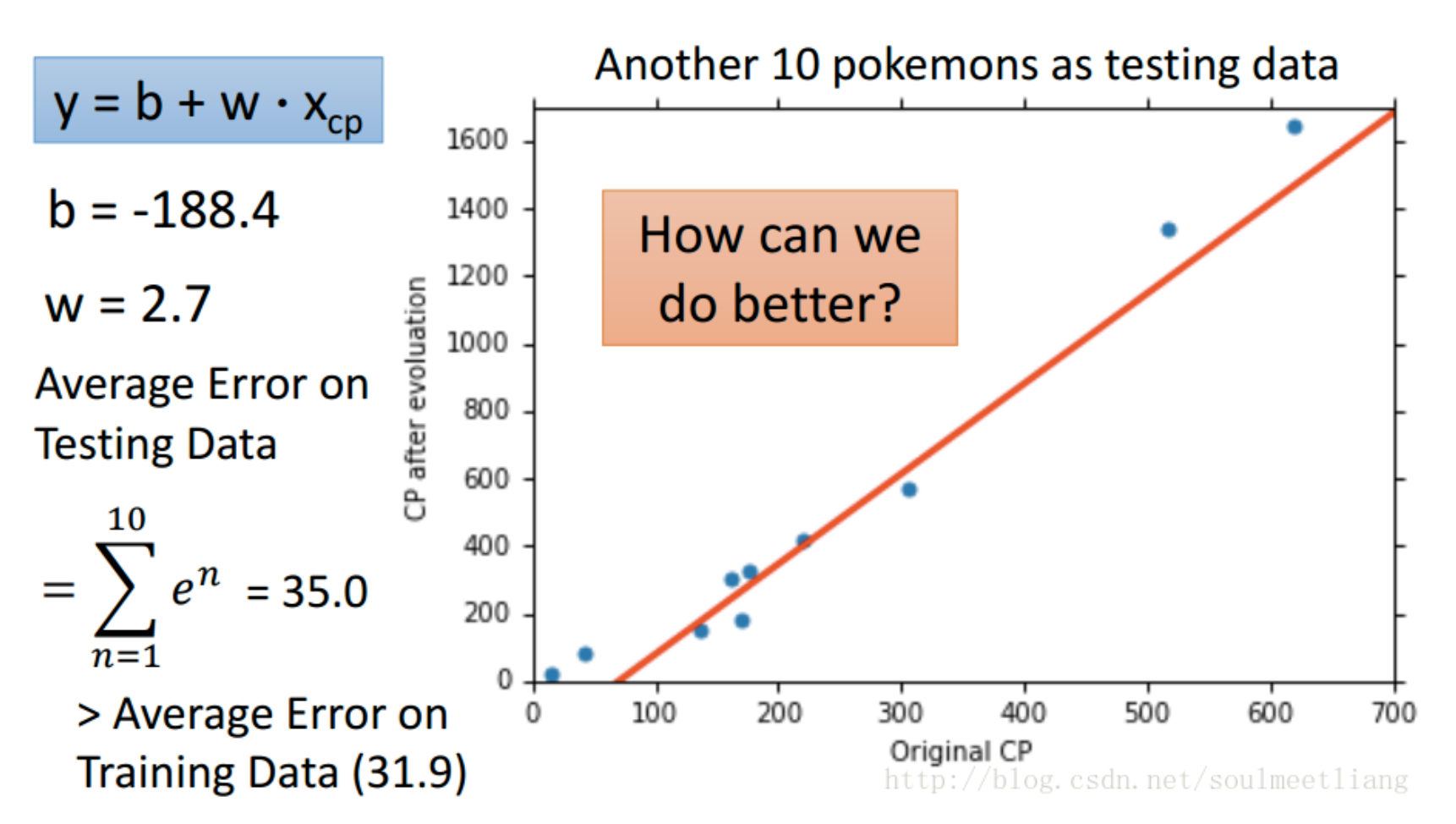
可以发现,并不是所有的点都能拟合函数,这就会造成很大的预测不准的情况,所以我们就要想办法优化。
优化
很容易想到,刚刚我们用了一次方程作为model,二次方程会不会更好一些呢,三次方程、四次方程呢?
于是我们做了以下实验,用同样的方法,放到多次方程中。
但是我们发现,预测的结果并不是随着f的复杂程度而提高。
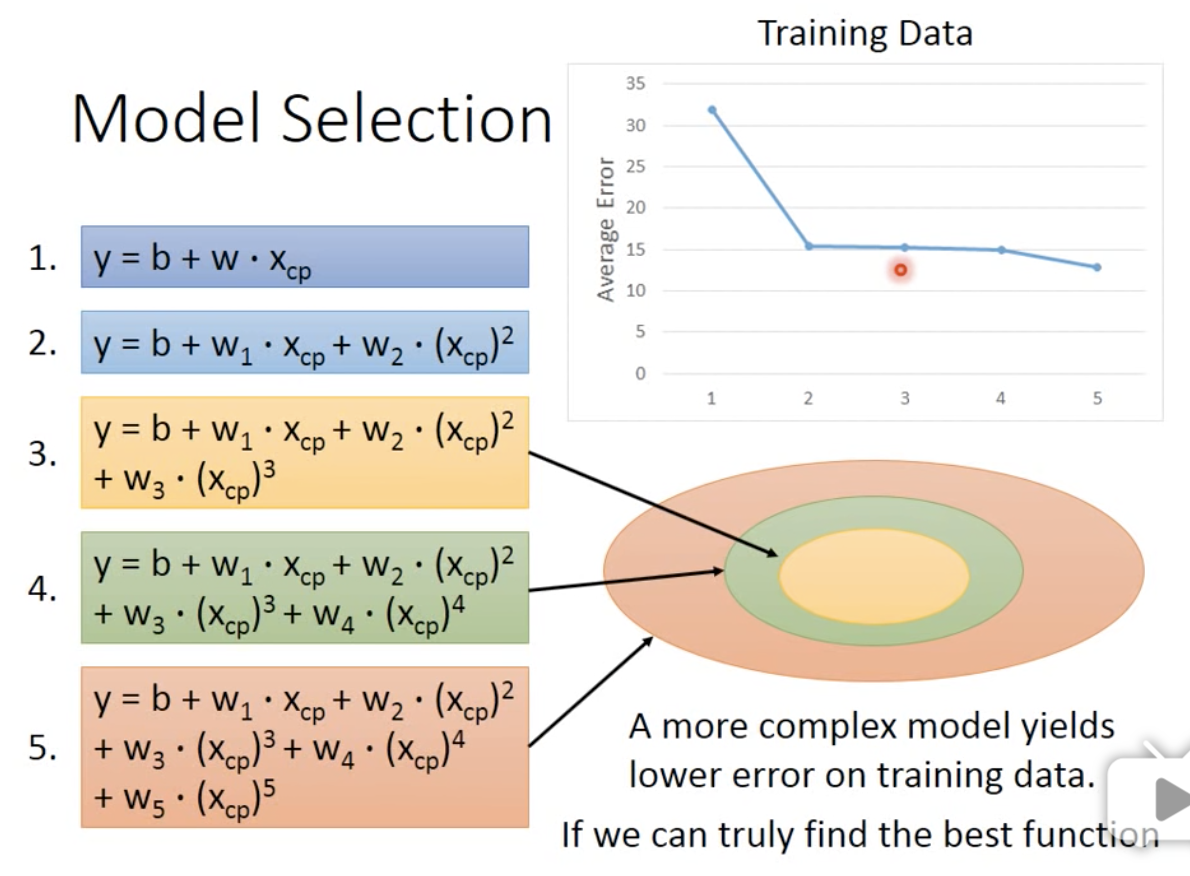
假设黄色的范围是是2元的f,绿色是 3元的f,那么更复杂的方程一定能覆盖到更简单的f。当f越来越复杂,在训练集上一定能找到更符合这个训练集的f。但是它们就不见得也能在测试集上取得同样的效果。

可以看到,在前三次时,都能随着f的复杂而提高测试集上侧准确率,但是在第四第五次时,就会崩溃。这就是过拟合。也就是说这个模型太适应训练集了,以至于没有迁移能力。所以,function不是越复杂越好,我们要选择一个最合适的。由上图可以看出,在三次方程中表现最好。
就好像一个学生,做到的考试题一直只有那几题,然后他就把答案背下来,这样当然在训练集中的准确率就非常高,但是一做到新的题,他就不会了,正确率就很低。
参考链接
https://blog.csdn.net/soulmeetliang/article/details/72619885
视频链接