Murphi入门（六）—— 用murphi实现GCD（3）

发表于 更新于 分类于 阅读次数：

该博文将继续从程序验证的角度对gcd的murphi程序进行修改， 本次修改的内容为：

  • 循环不变量
  • 迁移规则
  • ​gcd程序

循环不变量

概念

The loop invariants of the axiomatic approach go back to Floyd [1967] and Hoare [1969]. For this approach, a loop invariant is not just a quantity that remains unchanged throughout executions of the loop body (a notion that has also been studied in the literature), but more specifically an “inductive invariant”.

循环不变量是一种原子性的方法，来源于弗洛伊德和霍尔逻辑（见数理逻辑和程序验证）。循环不变量不仅是一个随循环过程而保持不变的值（尽管它字面如此），更确切地说，它是归纳不变量。这就说明了：

  • 初始状态时，循环不变量成立
  • 对第k个状态成立时，对第k+1个状态也成立

The invariant Inv plays no direct role in the informal semantics, but serves to reason about the loop and its correctness. Inv is a correct invariant for the loop if it satisfies the following conditions:

(1) Every execution of Init, started in the state preceding the loop execution, will yield a state in which Inv holds.

(2) Every execution of Body, started in any state in which Inv holds and Exit does not hold, will yield a state in which Inv holds again.

If these properties hold, then any terminating execution of the loop will yield a state in which both Inv and Exit hold. This result is a consequence of the loop semantics, which defines the loop execution as the execution of Init followed by zero or more executions of Body, each performed in a state where Exit does not hold. If Init ensures satisfaction of the invariant, and any one execution of Body preserves it (it is enough to obtain this property for executions started in a state not satisfying Exit), then Init followed by any number of executions of Body will.

循环不变量非形式句法中并不起作用，但是它从理论上保证了程序的执行（特别是循环）的正确性。满足以下两点，则是正确的循环变量：

  • 初始化时，inv是满足的
  • 在循环体内部执行时，在每个可达的状态，包括退出状态时，仍然会引导至一个满足inv的状态

结束循环的条件也仍然会保持满足inv

为什么要找循环不变量

如果我们知道如何使所有断言条件尽可能地强，如果我们学会如何推导出断言和程序，我们就不会犯这么多错误。我们知道程序是正确的，我们就根本不需要调试。花在运行测试用例，查看输出，查找错误的时间就可以大大减少。

  • 断言是指，每一个表判断，使得程序能够继续执行下去的语句，在程序中起判断作用。比如 x > 0 ， 这个断言的强度就低于 0 < x < 10。 越强的断言，范围越小，越精确。

前置条件 vs 后置条件

1
2
3
4
while precondition do
{
  executive body;
} until postcondition

前置条件即为循环开始时满足的条件，后置条件为循环结束时需满足的条件。即，在循环开始时，由于满足了某种条件，使得循环体得以执行；每次循环之后都检验一次循环的后置条件，如果满足后置条件，则结束循环。

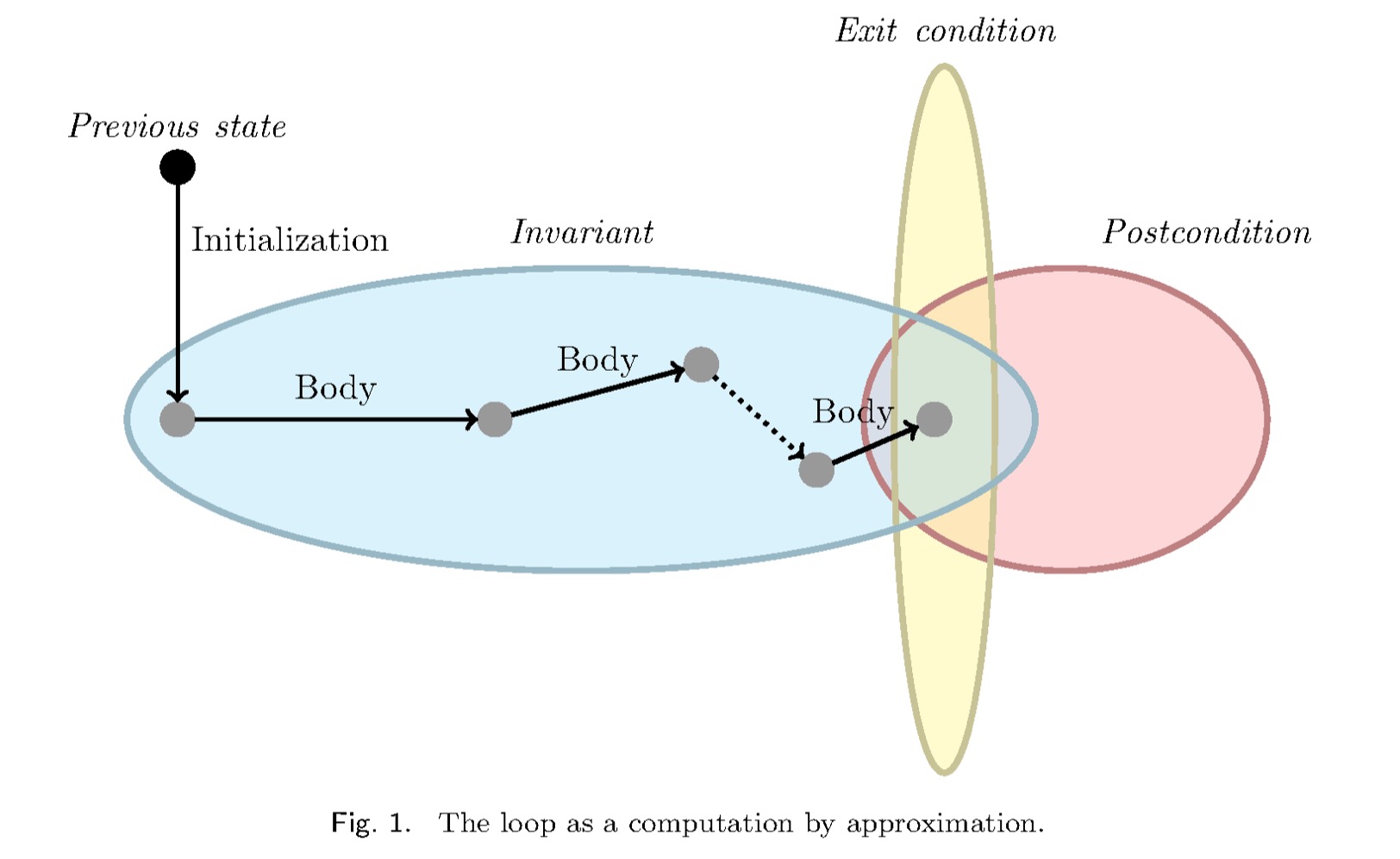
这就是从前置条件，经过循环，满足了结束条件，而退出循环的过程。其中可以看到，后置条件有很多，我们选择一个条件，作为退出条件即可。我们找循环不变量的方法，就是从后置条件中选择出循环不变量。

例子

我们仍旧以GCD为例子，通过前两次的修改，对GCD的理解已经比较深入了。这次将理解，建立在循环不变量上，首先要了解三个关于GCD的数学性质：

（其中，a，b是需要计算gcd的两个输入值。初始：Result=a，x=b）
$$
Result = x \wedge gcd(Result,x) = gcd(a,b)
$$

$$
gcd(x,x) = x
$$

$$
gcd(x,y) = gcd(x-y,y) \ for \ each\ x>y
$$

通过上面三个性质，我们可以将
$$
x > 0 \ &\ Result > 0\ &\ gcd(a,b) = gcd(Result,x)
$$
作为循环不变量。其中，前两个条件没什么好解释。对于第三个$gcd(a,b) = gcd(Result,x)$ ，我们先来看循环体内部：（伪代码，真正murphi代码见后文）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from
	Result := a ; x := b
invariant
	Result >0 x >0
	gcd (Result, x) = gcd (a, b) 
until
	Result = x
loop
	if Result > x then Result := Result − x
	else //Here x is strictly greater than Result x := x − Result
end
variant
	max (Result, x)
end

可以看到，循环的条件是Result ！= x（因为它写的是 until），然后执行计算gcd的过程。假设a = 18， b = 12， 则执行完之后，$Result = 6， x = 6，gcd(Result，x) = 6 = gcd（a，b）$ 。而在执行循环之前，$Result = a = 18, x = b = 12, gcd(Result, x) = gcd(a,b)$ 也成立。

具体实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
type 
    val_t: 0..30;
    
var
	a : val_t;
	b : val_t;
	Result : val_t;
	x : val_t;

function gcd(x,y: val_t):val_t;  -- 可以看到，把这个改成function，因为需要判断gcd的值
var
	r : val_t; 
	a : val_t;
	b : val_t;
begin
	a := x;
	b := y;
	r := a % b;
	while r!= 0 do
		a := b;
		b := r;
		r := a % b;
	end;
	return b;
end;


rule "loop"
	Result != x ==>
	begin
		while(Result != x) do
			if Result > x then
				Result := Result -x;
			else x := x - Result;
			end;
		end;
	end;

startstate
	a := 18;
	b := 12;
	Result := a;
	x := b;
end;

invariant "commonDivdors"
	(Result > 0) & (x > 0) & (gcd(Result,x)=gcd(a,b)) ;

运行结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
Verbose option selected.  The following is the detailed progress.

Firing startstate Startstate 0
Obtained state:
a:18
b:12
Result:18
x:12

------------------------------
Unpacking state from queue:
a:18
b:12
Result:18
x:12

The following next states are obtained:

Firing rule loop
Obtained state:
a:18
b:12
Result:6
x:6

------------------------------
Unpacking state from queue:
a:18
b:12
Result:6
x:6

The following next states are obtained:


==========================================================================

Result:

	Deadlocked state found.

State Space Explored:

	2 states, 1 rules fired in 0.10s.

可以看到，Result：6。正确

小结

可以看出，murphi虽然可以像其他程序语言一样执行计算任务，但别忘了它的主旨是验证。它的验证过程，相当于把别的程序看成其中的procedure和funciton，也就是murphi结构中的一部分。而它把对程序的验证步骤拆分成：初始化赋值，规则迁移，满足循环不变量，并用murphi进行编译和运行，遍历所有可能到达的状态，以此达到验证程序正确性的目的。

因此，验证步骤中，最重要的就是循环不变量。它刻画出程序正确的范围，找寻它是我们重要的工作。